Задачи на смекалку
Здесь будут размещаться разные задачи, требующие сообразительности. В разделе ШКОЛЬНЫЕ содержатся те из них, для решения которых достаточно школьных знаний. Другие задачи рассортированы по дисциплинам.
Решать их -- занятие очень полезное, т.к. вырабатывается навык придумывать новые способы решения (не во вселенском масштабе, конечно, а в масштабе собственного творческого архива). Это важно не только для того. чтобы быть хорошим инженером, но и просто для того, чтобы слыть башковитым человеком (женщиной или мужчиной).
Мои советы
Естественно и оправданно начинать с уже наработанных приемов. Но важно уметь не закапываясь глубоко, почувствовать, что выбранный, точнее тестируемый (в смысле пробуемый на вкус) путь заводит куда-то не туда: в тупик, на болото или в дремучий лес. Тогда надо сменить подход к решению задачи, попытаться взглянуть на нее иначе, как бы повертеть задачу на расстоянии вытянутой руки, фиксируя внимание на структуре, а не на деталях и мелочах. Хотя изредка бывает так, что кажущееся мелочью играет важную роль. Чобы повысить вероятность успеха, есть универсальный прием: комбинируйте все мыслимые сочетания подходов. В математике это звучно зовется методом Монте-Карло, а по-простому -- методом проб и ошибок.
О том, как это случается
Интересно было бы знать, каким образом решение трудной задачи приходит в голову, как возникает идея, наступает в определенном смысле прозрение. Но не думаю, что существует ответ на этот вопрос. Некоторые связывают этот процесс с чем-то внешним: не даром же говорят "Идея посетила/осенила меня, пришла в голову", в определенном смысле намекая на "шаловливый" космический разум (сегодня я добрый, а завтра фик тебе) или на что-то сверхестественное. По моему же твердому убеждению идеи рождаются внутри нас, это плод нашего собственного мыслительного процесса. Другое дело, что, как вообще в жизни, Господин Случай и в этом деле - заметная фигура: возникла ли в нашем мозгу та комбинация приемов, которая решает задачу, или не возникла далеко не всегда зависит от продолжительности и упорства размышлений. Важна сноровка и изобретательность в составлении всевозможных комбинаций. И это можно натренировать.
ДЕРЗАЙТЕ!
"ШКОЛЬНЫЕ" ЗАДАЧИ
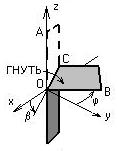
Задача 1 (возникла в связи с технологическим вариантом вибратора в проекте дипломницы Кузовкиной Е. )
Под каким углом b гнуть расположенную в плоскости x0z стальную полосу, чтобы отрезок ОА опустился на плоскость x0y под углом f=450 к оси 0y?
Примечание. Задачу можно решить по-школьному, зная только синусы, косинусы и теорему Пифагора. А можно по-взрослому, записав орты вдоль OА и OB, а также искомый вектор OC, и учитывая, что скалярное произведение векторов связано с косинусом угла между ними. Полезно пройти оба пути, чтобы прочувствовать насколько детский «путь» утомительней взрослого.
Задачи на "4" и "5" по дисциплине «антенны средств связи»
Задача 1 Антенна РЛС укрыта обтекателем. Его толщина d=2см. Коэффициент x затухания материала, из которого выполнен обтекатель, имеет квадратичную частотную зависимость вида
x(f)=0.5[нэп/(см ГГц2)] f2. В итоге КПД обтекателя соответствует выражению
КПД=exp(-2 x(f) d f2). Определите оптимальную частоту fОПТ, при которой коэффициент усиления (КУ=КНД*КПД) достигает максимального значения. Если Вам нужна площадь S раскрыва антенны, то пусть S=3м2.
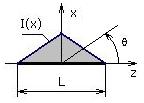
Задача 2
Получить выражение для ДН (строго говоря, для множителя системы) F(q) синфазного линейного излучателя с треугольным распределением тока I(z). Длина излучателя L.
Намек. Задачу можно решить двумя путями: • относительно рутинным – интегрированием с использованием приема интегрирования по частям; • или сообразив, что искомая ДН совпадает с ДН квадратного раскрыва в перпендикулярной плоскости, проходящей по диагонали квадрата.
Задача 3
Найти выражение для ДН (строго говоря, для множителя системы) F(q) равномерно и синфазно возбужденного линейного излучателя длины L с разрывом d в центре. На рисунке изображено распределение тока I(z).
Задачи на "4" и "5" по дисциплинам «Электродинамика и распространение радиоволн», «Электромагнитные поля и волны»
Задача 1 Докажите, что при произвольном соотношении амплитуд и фаз трех декартовых компонент вектора Е ничего сложнее обычной эллиптической поляризации не возникает. Т.е. годограф, вычерчиваемый вектором Е в пространстве, есть эллипс в некоторой плоскости (а не витееватая кривая на эллипсоиде, как это по началу кажется).












